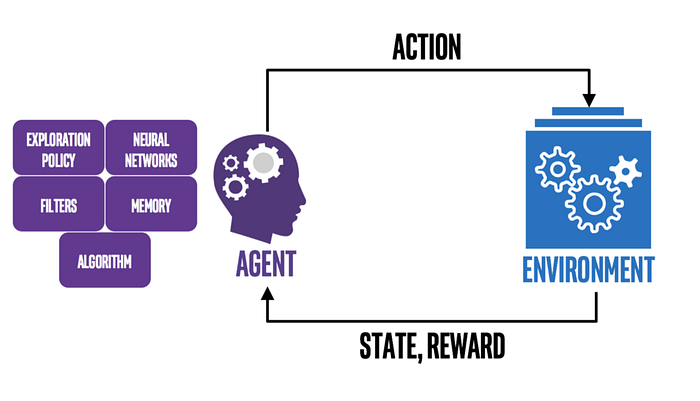
Q-learning is an off policy reinforcement learning algorithm that seeks to find the best action to take given the current state. It’s considered off-policy because the Q-Learning function learns from actions that are outside the current policy, like taking random actions, and therefore a policy isn’t needed. More specifically, Q-Learning seeks to learn a policy that maximizes the total reward.

Today we will try to find the shortest path connecting the Start and End Vertices, using Q-Learning and C Language. For our implementation, we have considered the following undirected unweighted graph –

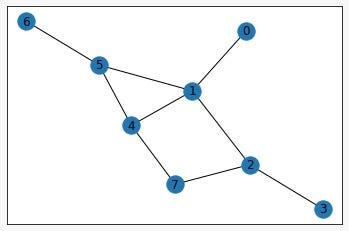
And for convenience, we have assumed the end vertex to be Node 7. Once you understand how the code works, you can modify the end vertex to any node you like, or even take it as an input from the user!

Let’s Code!!

We begin with including the required C libraries as well as defining a macro. Along with this, we will define certain global variables.

#include <stdio.h>
#include <stdlib.h>
#define RAN_LIM 500000

double qMatrix[8][8], rMatrix[8][8], gammaLR = 0.8;
int max_index[8], available_acts[8];
int ran_top = 0, ran[RAN_LIM];

Here, qMatrix is a 2D array which will represent our Q-Matrix. rMatrix is again a 2D array representing the rewards/points. Both of these matrices act like Adjacency Matrices for our Graph. We have chosen our learning rate to be 0.8 (gammaLR). We will understand the use of other parameters later as and when they are used.

Let us start our understanding with the main function. Initially all the required variables are initialized.

//Main Function Begins    int i, j;
    int initial_state, final_state = 7;
    int current_state, size_av_actions, action;
    double final_max=0.0, scores[100000], rMatrix[8][8], score=0.0;//Main Function Continued*

As mentioned earlier, we have restricted our final state to the 7th node (‘final_state’). While training the Q-Matrix, we need to keep track of the current state and the next state which is represented by ‘current_state’ and ‘action’ respectively. We shall understand the use of other variables later in the code.

In the following code, we are doing 3 things.

1. Firstly, we will take an initial state as input from the user.
2. Secondly, we will generate an array that will contain random numbers ranging from 0 to 7 (both inclusive).
3. And finally, we will fill in the values of the Q-Matrix as well as the R-Matrix according to the previously mentioned graph.

You may use any graph of your choice, but remember to change the inputs of the matrices accordingly. Our Q-Matrix will initially contain only 0 values. In our R-Matrix, we will put the value ‘0’ for adjacent nodes, ‘-1’ for non-adjacent nodes and ‘100’ for the cases where nodes are adjacent with Node-7 (Final Vertex). In short we are giving rewards to the paths that lead us to the Final Node (7).

//Main Function Continued*    //Input Initial State
    printf("Enter the initial state: ");
    scanf("%d",&initial_state);
    
    //Random Number from 0 to 7   
    for (int i = 0; i < RAN_LIM; i++)
    {
        ran[i] = rand() % 8;
    }


    for (i = 0; i < 8; i++)
    {
        for (j = 0; j < 8; j++)
        {
            rMatrix[i][j] = -1.0;
            qMatrix[i][j] = 0.0;

            if ((i == 0 && j == 1) || (i == 1 && j == 5) || (i == 5 && j == 6) || (i == 5 && j == 4) || (i == 1 && j == 2) || (i == 2 && j == 3) || (i == 2 && j == 7) || (i == 4 && j == 7) || (i == 1 && j == 4))
            {
                rMatrix[i][j] = 0.0;
            }

            if ((j == 0 && i == 1) || (j == 1 && i == 5) || (j == 5 && i == 6) || (j == 5 && i == 4) || (j == 1 && i == 2) || (j == 2 && i == 3) || (j == 2 && i == 7) || (j == 4 && i == 7) || (j == 1 && i == 4) )
            {
                rMatrix[i][j] = 0.0;
            }

            if ((i == 2 && j == 7) || (i == 7 && j == 7) ||(i == 4 && j == 7))
            {
                rMatrix[i][j] = 100.0;
            }
        }
    }//Main Function Continued**

Let us now take a look at our R-Matrix.

//Main Function Continued**    printf("\nPoints Matrix : \n");
    for (i = 0; i < 8; i++)
    {
        for (j = 0; j < 8; j++)
        {
            printf("%f\t",rMatrix[i][j]);
        }
        printf("\n");
    }
    printf("\n\n\n");

    printf("%f", rMatrix[7][7]);//Main Function Continued***

TRAINING

Our next move is to train the Q Matrix. Training is done in an iterative fashion (in our case 500 times).

//Main Function Continued***
    // Training the Q Matrix
    for (i = 0; i < 500; i++)
    {

        current_state = returnRandom();
        size_av_actions = available_actions(current_state,available_acts,rMatrix);
        action = sample_next_action(size_av_actions,available_acts);
        
        //printf("\nNext Step: %d\n", action);
        score = update(current_state, action,rMatrix,qMatrix);
        scores[i] = score;
        
        printf("\nScore : %f", score);
    }//Main Function Continued****

Lets take a look at its helper functions:

1. AVAILABLE ACTIONS:

For a random state (vertex) as a row value, this function will return all the possible column values whose R-Matrix value is greater than 0, for that specific row.

int available_actions(int state, int available_acts[],double rMatrix[][8])
{
    int k = 0, j = 0;
    while (j < 8)
    {
        if (rMatrix[state][j] >= 0.0)
        {
            available_acts[k] = j;
            k++;
        }
        j++;
    }
    printf("\n");
    return k;
}

2. SAMPLE NEXT ACTION:

This function will simply select a random index out of the previously returned array.

int sample_next_action(int size,int available_acts[])
{
    int a = returnRandom();
    int next_action = available_acts[a % size];
    return next_action;
}

2. UPDATE:

This is the most important function in our code.

Reinforcement Learning works on a random elements and checks if the chosen elements help us in getting a better solution.

This function follows a similar strategy. We start by finding out the non-zero values from the ‘action’ row of the Q-Matrix and storing them in an array (max_index). Next we randomly select one of those indices (index_of_max), and find the value from the Q-Matrix (max_value) where the row value is ‘action’ and column value is ‘index_of_max’ .

Finally we will conduct our main updation process and return back the score where the learning rate is 0.8.

Notice that until the ‘max_value’ is zero, the updation does not take place. Hence only after a few random iterations the updation process will begin.

double update(int current_state, int action, double rMatrix[][8],double qMatrix[][8])
{
    int i = 0, j = 0, k = 0, index_of_max;
    double temp_max = 0.0, max_value = 0.0, sumA = 0.0;

    //Collecting all the indices where we have max in action row
    for (i = 0; i < 8; i++)
    {
        max_index[i] = 0;

        if (temp_max == qMatrix[action][i])
        {
            max_index[j] = i;
            j++;
        }
        else if (temp_max < qMatrix[action][i])
        {
            j = 0;
            temp_max = qMatrix[action][i];
            max_index[j] = i;
            j++;
        }
    }

    //Select a random out of all maximum
    int a = returnRandom() % j;
    index_of_max = max_index[a];
    
    max_value = qMatrix[action][index_of_max];


    //Main updation
    qMatrix[current_state][action] = rMatrix[current_state][action] + (gammaLR * max_value);
    temp_max = 0.0;
    for (i = 0; i < 8; i++)
    {
        for (j = 0; j < 8; j++)
        {
            if (qMatrix[i][j] > temp_max)
            {
                temp_max = qMatrix[i][j];
            }
        }
    }

    //printf("\nQ Max: %d", temp_max);
    //printArray(qMatrix);
    if (temp_max > 0)
    {
        for (i = 0; i < 8; i++)
        {
            for (j = 0; j < 8; j++)
            {
                sumA = sumA + (qMatrix[i][j] / temp_max);
            }
        }

        sumA = sumA * 100;
        return sumA;
    }
    else
    {
        return 0.0;
    }
}

NORMALIZATION

After the training is completed, we will find the maximum value from the Q-Matrix so that while displaying our trained Q-Matrix, we can display the normalized values.

//Main Function Continued****        //Finding the Max
    for (i = 0; i < 8; i++)
    {
        for (j = 0; j < 8; j++)
        {
            if (final_max < qMatrix[i][j])
            {
                final_max = qMatrix[i][j];
            }
        }
    }


    printf("\n\nTrained Q Matrix: \n");
    for (i = 0; i < 8; i++)
    {
        for (j = 0; j < 8; j++)
        {
            printf("%f\t", (qMatrix[i][j] / final_max * 100.0));
        }
        printf("\n");
    }//Main Function Continued*****

FINDING OPTIMAL PATH

Our final step is to find the optimal path to Node 7

int curr_state=initial_state;
    int visited[8]={0,0,0,0,0,0,0,0};
    int no_way=0;
    int row_max=0,max_ind=0;

    printf("Path: \n");
    while (visited[final_state]!=1)
    {
        printf("%d-> ",curr_state);
        row_max=0;
        max_ind=0;    
        
        for(int i=0;i<8;i++)
        {
            if(visited[i]==0)
            {
                if(qMatrix[curr_state][i]>row_max)
                {
                    max_ind=i;
                    row_max=qMatrix[curr_state][i];
                }
            }
        }

        curr_state=max_ind;
        visited[max_ind]=1;
        if(row_max==0)
        {
            no_way=1;
            break;
        }
        
        if(curr_state==final_state)
        {
            break;
        }
    }
    
    if(no_way==1)
    {
        printf("%d | There's no way after this\n");
    }
    else
    {
        printf("%d is the shortest path\n",curr_state);
    }

Here the ‘visited’ array tells us if the index node has been traversed over or not.

The basic principle behind the finding the optimal path is as follows; We start by finding out the max value in the row (initially the row value will be the initial state) of the Q-Matrix and store its column value. This column value is used as a row value for the next max element search, after which we again store the column value. This process is continued until we reach the final node, Node 7.

Printing out the steps will give us the shortest path from the User Entered Vertex and End Vertex.

SAMPLE OUTPUT

References/Links:

1. Complete Code — Github
2. YouTube
3. Python Code

Authors:

1. Soham Bhure
2. Mihir Tale
3. Tanya Agrawal
4. Ganesh Tarone